 |
| Tipos de Cartas de Control usadas en Six Sigma y para qué se usan |
TODO LO QUE DEBERÍAS SABER SOBRE CARTAS DE CONTROL
Hablar de Cartas de Control en Six Sigma es hablar de la variación dentro de un proceso.
La variación en las características de un producto o servicio es parte natural del proceso que lo produce, aún operando correctamente el resultado de un proceso siempre tendrá algo de
variación.
Este tipo de variación, en mayor o menor medida siempre estará, pero su
comportamiento será "predecible".
Por otra parte también existe otro tipo de variación, de origen más
repentino, sorpresivo e impredecible, que tendrá consecuencias sumamente
indeseables para la satisfacción del cliente y en consecuencia para
el negocio en su conjunto.
Estas dos fuentes o causas de variación de un proceso pueden identificarse como:
👉 Causas comunes, responsables de la variación natural del proceso.
Estas dos fuentes o causas de variación de un proceso pueden identificarse como:
👉 Causas comunes, responsables de la variación natural del proceso.
👉 Causas especiales o asignables, responsables de la variación anormal, no esperada, sorprersiva, de ocurrencia poco común del proceso.
Inicialmente, para mejorar significativamente la satisfacción del cliente, será clave que la pyme se enfoque en identificar y eliminar la variación debida a causas especiales.
|
|
Figura 1: características y ejemplos de causa común y especial de
variabilidad |
EL CONTROL ESTADÍSTICO DE PROCESO.
La estrategia de monitoreo de la variación de un proceso es el Control Estadístico de Proceso (CEP o SPC en inglés), también conocido en Six Sigma como Evaluación Numérica de Métricas o NEM por su acrónimo en inglés.
En ella el foco está puesto en hacer un seguimiento minucioso de la
variación y es especialmente en detectar LO ANTES POSIBLE aquella que se
deba a causas especiales.
La herramienta de medición por excelencia para lograr ese cometido es la Carta de Control; la cuál te dirá si el proceso está o no bajo control (estabilizado).
La herramienta de medición por excelencia para lograr ese cometido es la Carta de Control; la cuál te dirá si el proceso está o no bajo control (estabilizado).
La carta de control es una herramienta sumamente operativa para la rápida
toma de decisiones en el proceso productivo, por lo tanto será de vital
importancia que se encuentre donde se tomen esas decisiones, es decir en
el piso, al alcance de los operadores e inclusive que sean ellos los
encargados de graficarla.
Pero ojo! se deberá tener presente que un
proceso bajo control significará que solo tendrá una cantidad de
variación predecible y estable (causa común), lo que no significará que
esa cantidad de variación sea la deseable.
Para averiguarlo tendrás que comparar la variación contra las
especificaciones del cliente a través de un Análisis de Capacidad de Proceso, tema que no se tratará en esta
entrada pero que bien amerita otra publicación que seguramente en algún
momento subiré.
Llegado a este punto quizás te estés preguntando...
Llegado a este punto quizás te estés preguntando...
QUÉ ES UNA CARTA DE CONTROL
Una carta de control muestra graficamente estadísticas claves del proceso
con el fin de ayudarte a diferenciar el origen de la variabilidad.
Esas estadísticas incluyen observaciones individuales, medias de subgrupos, estadísticos ponderados y números de defectos.
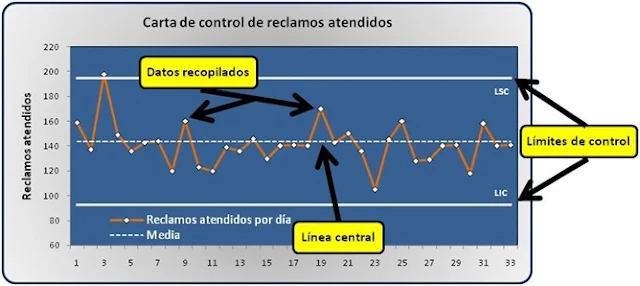
Los elementos principales de una carta de control son los datos graficados, los límites de control y la línea central, como podras apreciarlo en la siguiente figura.
Esas estadísticas incluyen observaciones individuales, medias de subgrupos, estadísticos ponderados y números de defectos.
Los elementos principales de una carta de control son los datos graficados, los límites de control y la línea central, como podras apreciarlo en la siguiente figura.
|
|
Figura 2: elementos principales de una carta de control |
Los puntos en una carta de control representan los datos graficados en
orden cronológico.
Estos puntos pueden representar tanto datos continuos como discretos
(atributos).
Cada punto representa una medida “individual” (tiempo de
tramitación de cada pedido) o algún cálculo basado en varios
“datos agrupados” (porcentaje de artículos defectuosos por
lote).
Línea central (LC) es la media de los datos graficados.
Límites de control (LSC “superior”, LIC “inferior”), delimitan la
variación esperada para un proceso y por convenio se los representa a
3 desviaciones estándar de la media.
Su figura dará una idea de la capacidad del proceso de entregar los
resultados esperados y será indispensables para detectar causas especiales
de variación.
Si un proceso está fuera de control se evidencia en la gráfica como patrones poco comunes o incluso puntos fuera de los límites de control.
Se dice entonces que hay variación por causas especiales y en consecuencia el proceso no está bajo control o estabilizado.
Para complementar la lectura te recomiendo visitar en este blog “Las 7 Herramientas de Ishikawa de la Calidad”.
Si un proceso está fuera de control se evidencia en la gráfica como patrones poco comunes o incluso puntos fuera de los límites de control.
Se dice entonces que hay variación por causas especiales y en consecuencia el proceso no está bajo control o estabilizado.
Para complementar la lectura te recomiendo visitar en este blog “Las 7 Herramientas de Ishikawa de la Calidad”.
Ahora bien, esta simple y a la vez potente herramienta no se trata de un
solo tipo de gráfica.
QUÉ TIPOS DE CARTAS DE CONTROL HAY
Comúnmente disponemos de aproximadamente media docena de diferentes tipos
de cartas de control para ser utilizadas según la ocasión.
Para facilitarte las cosas voy a empezar por mostrarte un arbol de selección de cartas de control en dónde encontrarás todas las gráficas que luego explicaré, con el fín de guiarte en tu comprensión del tema y, sobre todo, en la elección de la carta de control correcta.
Para facilitarte las cosas voy a empezar por mostrarte un arbol de selección de cartas de control en dónde encontrarás todas las gráficas que luego explicaré, con el fín de guiarte en tu comprensión del tema y, sobre todo, en la elección de la carta de control correcta.
No están todas, pero sí las más frecuentemente utilizadas.
|
|
Figura 3: árbol de selección de cartas de control. |
Es mi intención en esta entrada hablarte de ellas, ya que no siempre
se conoce fehacientemente de qué tipos de graficas de control
disponemos y sobre todo, por qué, cuándo y cómo utilizarlas.
BENEFICIOS DEL CONTROL ESTADISTICO DE PROCESO
El CEP no debería faltar en ninguna pyme industrial, sobre todo en
aquellos procesos que sean vitales para sus clientes.
Le brindará diversos y variados beneficios, todos ellos muy
relacionados con la satisfacción del cliente.
Su implementación no es complicada, aunque sí requerirá de un alto
nivel de disciplina y constancia para que sea exitosa.
Los principales beneficios serán:
✔ Se reducen los costos de manufactura.
✔ Se logran procesos estables.
✔ Mejora la calidad de los productos y servicios.
✔ Facilitan la fijación de especificaciones realistas de productos y servicio.
✔ Se reduce la inspección.
✔ Minimizan el tiempo muerto entre el problema y la solución.
✔ Mejora la relación con el cliente, la pyme opera de manera más confiable y predecible.
✔ Los tiempos de ciclo se reducen.
Ellos pueden ser de dos clases: datos continuos o datos de atributos.
Por ejemplo, una variable continua es el peso de un producto y una variable de atributos puede ser la categoría "pasa" y "no pasa" o también el “número de defectos en una muestra”.
Las mediciones continuas normalmente proporcionan más información que los datos de atributos, pero los datos de atributos, por lo general, son más fáciles de recopilar y por lo tanto se los elige cuando las mediciones continuas son difíciles de obtener.
Vayamos primero por el lado de los datos continuos; aquí se impone la siguiente pregunta:
La carta R o S muestra el cambio o las variaciones “dentro” de los subgrupos a lo largo del proceso, mientras que la carta X-barra muestra la variación "entre" los subrupos
Entonces en este punto la pregunta a hacer es la siguiente:
A2, D3, D4: son constantes pre definidas usadas en las técnicas de cartas de control.
Esta estrategia de control se sigue especialmente cuando:
Importante que notes que lo límites de control son cambiantes, eso es consecuencia de los distintos tamaños de muestra con los que trabaja esta gráfica.
Por lo tanto los pasos a seguir para hacer la gráfica u son similares a la gráfica c, pero teniendo en cuenta las siguientes diferencias:
El valor que se lleva al gráfico es el número medio de defectos por unidad y los límites no son fijos sino que dependerán del tamaño de la muestra.
✔ Se logran procesos estables.
✔ Mejora la calidad de los productos y servicios.
✔ Facilitan la fijación de especificaciones realistas de productos y servicio.
✔ Se reduce la inspección.
✔ Minimizan el tiempo muerto entre el problema y la solución.
✔ Mejora la relación con el cliente, la pyme opera de manera más confiable y predecible.
✔ Los tiempos de ciclo se reducen.
✔ Permiten disponer de
Estándares permanentemente corregidos
Ahora bien, una vez convencido, cómo sigue la historia.
Ahora bien, una vez convencido, cómo sigue la historia.
Volviendo a ver la figura 3 surge una pregunta clave a plantear y
contestarse:
TIPOS DE DATOS
La gráfica de control que vayas a utilizar dependerá estrechamente de la clase de datos que recopiles.Ellos pueden ser de dos clases: datos continuos o datos de atributos.
👉 Datos continuos.
Son del tipo numérico.
Tienen un número infinito de valores.
Suelen incluir valores fraccionados o decimales.
Su medición es objetiva.
👉 Datos de atributos o categóricos.
Están restringidas a categorías especificadas o valores discretos.
No hablan de cantidades sino más bien de cualidades del producto o
servicio.
Sa medición es subjetiva.
Por ejemplo, una variable continua es el peso de un producto y una variable de atributos puede ser la categoría "pasa" y "no pasa" o también el “número de defectos en una muestra”.
Las mediciones continuas normalmente proporcionan más información que los datos de atributos, pero los datos de atributos, por lo general, son más fáciles de recopilar y por lo tanto se los elige cuando las mediciones continuas son difíciles de obtener.
Vayamos primero por el lado de los datos continuos; aquí se impone la siguiente pregunta:
¿DATOS AGRUPADOS O NO AGRUPADOS?
Pero antes de continuar será oportuno repasar
qué es un subgrupo.
Por ejemplo, en una troqueladora que produce 100 piezas por hora, el analista de control de calidad decide medir cada hora, cinco piezas seleccionadas de manera aleatoria.
Decimos entonces que cada muestra de cinco piezas es un subgrupo.
La intención al trabajar con subgrupos es incluir toda la variación común dentro de cada subgrupo y dejar que la variación por causas especiales se manifieste entre los subgrupos.
Por ello un criterio para elegir subgrupos es que las diferencias entre mediciones dentro del mismo subgrupo sean pequeñas y que te permita detectar diferencias entre subgrupos.
Para los estudios iniciales del proceso, los subgrupos de 4 o 5 unidades que se recopilan más o menos cada hora son habituales, pero también es posible encontrarse con subgrupos de mayor tamaño, lo cual será determinante en cuanto a la elección del tipo de gráfica a utilizar.
Es importante resaltar que las cartas de control para datos agrupados (o para datos individuales) parten del supuesto de que su comportamiento se ajusta a la normalidad.
Moderadas desviaciones de ese comportamiento no invalida las cartas de control.
Por ejemplo, en una troqueladora que produce 100 piezas por hora, el analista de control de calidad decide medir cada hora, cinco piezas seleccionadas de manera aleatoria.
Decimos entonces que cada muestra de cinco piezas es un subgrupo.
Un subgrupo es un pequeño grupo de unidades que se crean bajo el mismo conjunto de condiciones y entradas, y que representa una "instantánea" del proceso.Las mediciones dentro de un subgrupo deben tomarse muy cercanas en el tiempo, y deben seguir siendo independientes unas de otras.
La intención al trabajar con subgrupos es incluir toda la variación común dentro de cada subgrupo y dejar que la variación por causas especiales se manifieste entre los subgrupos.
Por ello un criterio para elegir subgrupos es que las diferencias entre mediciones dentro del mismo subgrupo sean pequeñas y que te permita detectar diferencias entre subgrupos.
Para los estudios iniciales del proceso, los subgrupos de 4 o 5 unidades que se recopilan más o menos cada hora son habituales, pero también es posible encontrarse con subgrupos de mayor tamaño, lo cual será determinante en cuanto a la elección del tipo de gráfica a utilizar.
Es importante resaltar que las cartas de control para datos agrupados (o para datos individuales) parten del supuesto de que su comportamiento se ajusta a la normalidad.
Moderadas desviaciones de ese comportamiento no invalida las cartas de control.
Esa tolerancia es mayor cuando trabajamos con datos agrupados en lugar de
datos individuales, y es esa una razón de peso que explica la preferencia
por los datos agrupados siempre que sea posible.
DATOS CONTINUOS Y AGRUPADOS: CARTAS DE CONTROL X BARRA-R Y X BARRA-S
Aquí la característica a conocer es qué tamaño tiene el subgrupo.
Dependiendo de ello será el tipo de carta de control que vayas a
utilizar.
Para agrupamientos iguales o inferiores a 8 datos las gráficas que se utilizan son las X barra-R, y para subgrupos mayores a los 8 datos se opta por las cartas de control X barra-S.
Cabe aclarar que...
Para agrupamientos iguales o inferiores a 8 datos las gráficas que se utilizan son las X barra-R, y para subgrupos mayores a los 8 datos se opta por las cartas de control X barra-S.
Cabe aclarar que...
un proceso en el que se está controlando una característica continua, puede abandonar su estado de control por verse afectada su media, su variabilidad o ambas.
Por consiguiente se construyen gráficas para controlar ambos parámetros
por separado, no solo la media.
Pero qué significa cada una de las graficas arriba mencionadas.
Carta de control X barra, es la grafica de los
promedios de cada subgrupo.
Carta de control R, es la gráfica de los rangos de cada
subgrupo (n ≤ 8)
Carta de control S, es la gráfica de los
desvíos estándar de cada subgrupo (n > 8).
La carta R o S muestra el cambio o las variaciones “dentro” de los subgrupos a lo largo del proceso, mientras que la carta X-barra muestra la variación "entre" los subrupos
Entonces en este punto la pregunta a hacer es la siguiente:
¿Es consistente la variación en las mediciones dentro de los
subgrupos?
Las mediciones dentro de un subgrupo serán consistentes y estables solo cuando la carta R o S estén en control.
Esto incrementará la “sensibilidad” de la Carta de Control, aumentando su capacidad de detectar anormalidades de manera más rápida.
En cada una de las gráficas un punto representa a un subgrupo, como se muestra en la figura 4.
Las mediciones dentro de un subgrupo serán consistentes y estables solo cuando la carta R o S estén en control.
Es condición necesaria que la carta R o S esté en control para luego sí, dibujar la carta X-barra.Ten en cuenta que si el tamaño del subgrupo aumenta, los límites de control tienden a acercarse.
Esto incrementará la “sensibilidad” de la Carta de Control, aumentando su capacidad de detectar anormalidades de manera más rápida.
En cada una de las gráficas un punto representa a un subgrupo, como se muestra en la figura 4.
|
||
|
Figura 4: cartas de control Xbarra-R/S (hechas con Minitab) |
- Definiciones y fórmulas.
|
A2, D3, D4: son constantes pre definidas usadas en las técnicas de cartas de control.
|
|
Figura 5: tabla de cosntantes usadas para calcular límites de
control |
DATOS CONTINUOS INDIVIDUALES: CARTA DE CONTROL I-mR
Cuando no es posible o aconsejable trabajar con datos agrupados, se opta por trabajar con el set de gráficas I - mR.
Carta de control I, es la grafica de los valores de las
observaciones individuales de la variable evaluada.
Carta de control mR, es la gráfica de los rangos móviles.
Esta estrategia de control se sigue especialmente cuando:
📌 Sólo existe la oportunidad de tomar una muestra (proceso
batch).
📌
La variación dentro de un subgrupo “natural” es de poca preocupación (la
variación “Dentro” es mucho menor que la variación “Entre”).
📌
Los conocimientos sobre un proceso son escasos.
|
|
Figura 6: cartas de control I-mR para datos continuos
individuales |
- Definiciones y fórmulas.
d2: es una constante pre definida usada en técnicas de cartas de control
(ver figura 5).
Ahora bien, si nos movemos en sentido contrario en la parte superior del árbol de selección (Figura 3), tenemos otro tipo de datos, los que necesitarán de una familia distinta de cartas de control.
Ahora bien, si nos movemos en sentido contrario en la parte superior del árbol de selección (Figura 3), tenemos otro tipo de datos, los que necesitarán de una familia distinta de cartas de control.
DATOS SOBRE ATRIBUTOS: GRAFICAS DE CONTROL P, nP, u y c
En este caso la característica de calidad que se deseas evaluar no es
medible en el sentido tradicional, sino que es cierto atributo que puede o
no poseer, el producto o servicio.
Esta información responde a distribuciones de probabilidad de tipo Binomial o de Poisson, a diferencia de los casos anteriores que ajustaban a distribuciones de tipo normal.
Un punto clave a tener en cuenta cuando se trabaja con esta clase de datos es el criterio a seguir para definir si un individuo tiene o no la característica evaluada.
Este criterio debe ser claro y no debe cambiar mientras se mantiene los límites de control, caso contrario se deberá recalcular los límites y empezar de cero.
En esta "rama" del arbol de selección lo primero que debes preguntarte es si tus datos van sobre defectos por unidad o sobre elementos defectuosos.
Esta información responde a distribuciones de probabilidad de tipo Binomial o de Poisson, a diferencia de los casos anteriores que ajustaban a distribuciones de tipo normal.
Un punto clave a tener en cuenta cuando se trabaja con esta clase de datos es el criterio a seguir para definir si un individuo tiene o no la característica evaluada.
Este criterio debe ser claro y no debe cambiar mientras se mantiene los límites de control, caso contrario se deberá recalcular los límites y empezar de cero.
En esta "rama" del arbol de selección lo primero que debes preguntarte es si tus datos van sobre defectos por unidad o sobre elementos defectuosos.
GRAFICAS PARA ELEMENTOS DEFECTUOSOS (CARTAS DE CONTROL P Y Np)
Para situarte en la problemática piensa en lo siguiente:
¿Cada unidad es defectuosa o no?
Estos gráficos se utilizan cuando los individuos de un proceso se
clasifican en
defectuoso-no defectuoso, sano-enfermo, dentro-fuera de tolerancia,
etc y se desea controlar la proporción p de individuos en uno de
estos grupos.
Las graficas que se utilizan en este caso son las cartas de control P y
nP.
Carta de control P: monitorea la proporción (o el porcentaje) de
elementos defectuosos.
Carta de control nP: monitorea la cantidad de defectos en una
muestra o proceso
Gráfica p
Se aplica a casos en donde el tamaño de la muestra puede ser variable a
lo largo del seguimiento.
La magnitud de dichas muestra deben ser lo suficientemente grande como
para dar oportunidad de que aparezcan al menos tres o cuatro unidades
defectuosas.
Un tamaño típico de muestra es de unas 100 observaciones.
Un tamaño típico de muestra es de unas 100 observaciones.
|
| Figura 7: carta de control P para datos de atributos (hecho con Minitab) |
Importante que notes que lo límites de control son cambiantes, eso es consecuencia de los distintos tamaños de muestra con los que trabaja esta gráfica.
- Definiciones y fórmulas.
Gráfica nP.
Esta carta de control se aplica al mismo tipo de problema que en el caso
anterior, pero con el tamaño de muestra fijo.
|
|
Figura 8: carta de control nP para datos de atributos (hecho con
Minitab) |
- Definiciones y fórmulas.
GRAFICAS PARA DEFECTOS POR UNIDAD (CARTAS DE CONTROL C Y U)
Ahora para situarte en la problemática piensa en lo siguiente:
¿Cada unidad puede tener múltiples defectos o no?
Aquí estamos interesados en monitorear el número de defectos que aparecen
en un individuo.
Este estudio es más completo que el anterior porque:
Este estudio es más completo que el anterior porque:
👉 El individuo puede no ser defectuoso y presentar defectos.
El carácter defectuoso puede ser de distinta magnitud dependiendo de la
cantidad de defectos que presente.
Carta de control C
Es para aquellos casos en donde te interese seguir de cerca el número de
defectos por cierta unidad predefinida, como ser hora, metro cuadrado,
kilómetro, etc
Este tipo de gráfica se construye asumiendo una distribución según la ley de Posisson, con λ como número medio de ocurrencia por unidad de tiempo, superficie, volumen, etc.
Este tipo de gráfica se construye asumiendo una distribución según la ley de Posisson, con λ como número medio de ocurrencia por unidad de tiempo, superficie, volumen, etc.
|
| Figura 9: Carta de control C para el n° de defectos de estampación por m2 en un proceso textil (hecho con Minitab) |
-
Definiciones y fórmulas.
Carta de control U
El universo de aplicación es el mismo que el caso anterior, número de
defectos que aparecen en la unidad o individuo, pero la diferencia radica
que tratamos con problemáticas en donde no es posible tomar una unidad del
mismo tamaño para controlar el número de defectos.
Por ejemplo, puede ser difícil tomar 1 m2 de tela para controlar, por lo que se toman piezas de aproximadamente 1 m2.
En el control de la cantidad de personas que pasan por una máquina registradora, en lugar de tomar intervalos de tiempo iguales se toman intervalos más flexibles.
Cuando se mide el número de defectos por lote, éste pueda que no tenga un número fijo de individuos.
Aquí también se sigue la distribución de la ley de Poissson con:
Por ejemplo, puede ser difícil tomar 1 m2 de tela para controlar, por lo que se toman piezas de aproximadamente 1 m2.
En el control de la cantidad de personas que pasan por una máquina registradora, en lugar de tomar intervalos de tiempo iguales se toman intervalos más flexibles.
Cuando se mide el número de defectos por lote, éste pueda que no tenga un número fijo de individuos.
Aquí también se sigue la distribución de la ley de Poissson con:
Y la media de u será:
Por lo tanto los pasos a seguir para hacer la gráfica u son similares a la gráfica c, pero teniendo en cuenta las siguientes diferencias:
El valor que se lleva al gráfico es el número medio de defectos por unidad y los límites no son fijos sino que dependerán del tamaño de la muestra.
10 PASOS PARA CONSTRUIR UNA CARTA DE CONTROL
- Selecciona la métrica que vas a graficar (características del producto o servicio, parámetros del proceso).
- Determina el propósito de la carta.
- Selecciona el tipo de carta de control a utilizar.
- Determina los métodos y criterios de medición.
- Define el plan de muestreo (tamaño de la muestra, intervalos y frecuencias de muestreo).
- Calcula la línea central (valor medio).
- Establece las bases para calcular los límites de control.
-
Ajusta los formatos para recolectar los datos y graficarlos.
- Prepara instrucciones escritas para cada fase.
-
Realiza el entrenamiento necesario de las personas directamente
involucradas.
LOS LÍMITES DE CONTROL…
❗ Son una medición de lo qué es o ha sido el proceso, es decir es el pasado
o el presente, NO el futuro o lo que deseas que el proceso haga.
❗ Se calculan a partir de una serie temporal de la variable de medición.
❗ No necesitan ser recalculados cada vez que se recopila un dato.
❗ Son una funcion del plan de muestreo y del criterio de subagrupación, al igual que las mediciones observadas.
❗ No tienen nada que ver con los estandares ni tampoco son especificaciones.
❗ Evidencian el grado de variación que existe.
❗ No necesitan ser recalculados cada vez que se recopila un dato.
❗ Son una funcion del plan de muestreo y del criterio de subagrupación, al igual que las mediciones observadas.
❗ No tienen nada que ver con los estandares ni tampoco son especificaciones.
❗ Evidencian el grado de variación que existe.
Bueno estimado lector, si has llegado hasta acá te lo agradezco
mucho.
Me propuse con este post darte claridad sobre qué son las cartas de
control, qué tipos hay y cuál de ellas seleccionar conforme a la
situación.
Espero haberlo logrado.
Ahora te toca a ti.
¿Te quedaron inquietudes, sugerencias, preguntas, opiniones, pedidos de temáticas o incluso correcciones de cosas que se me hayan pasado?
No lo dudes y envíame un comentario, me encantaría leerte y corresponderte.
Escribo para ayudar a mejorar, sobre todo a aquellas pequeñas pymes sin departamentos de mejora continua, y me encanta hacerlo, pero también quiero aprender a hacerlo cada vez mejor.
Si deseas saber más de mí, te invito a contactar en LinkedIn o si lo prefieres, podrás escribirme a: kaizenizar@gmail.com
Que tengas una buena semana. Hasta pronto!
Pablo
¿Te quedaron inquietudes, sugerencias, preguntas, opiniones, pedidos de temáticas o incluso correcciones de cosas que se me hayan pasado?
No lo dudes y envíame un comentario, me encantaría leerte y corresponderte.
Escribo para ayudar a mejorar, sobre todo a aquellas pequeñas pymes sin departamentos de mejora continua, y me encanta hacerlo, pero también quiero aprender a hacerlo cada vez mejor.
Si deseas saber más de mí, te invito a contactar en LinkedIn o si lo prefieres, podrás escribirme a: kaizenizar@gmail.com
Que tengas una buena semana. Hasta pronto!
Pablo
